弹性力学三大方程
为了由弹性力学问题中的已知量求出未知量,必须建立这些已知量与未知量之间的关系,以及各个未知量之间的关系,从而导出一套求解的方程。在导出方程时,可以从三个方面来进行分析。一方面是静力学方面,由此建立应力、体力、面力之间的关系。另一方面是几何学方面,由此建立形变、位移和边界位移之间的关系。再一个是物理学方面,由此建立形变与应力之间的关系。
平衡方程
在 P 点附近取出一个微小的正平行六面体PACB,它在 x 和 y 方向的尺寸分为为 dx 和 dy,在 z 方向的尺寸为单位长度 1,此正平行六面体又称微元体,进行应力分析,如下图所示。
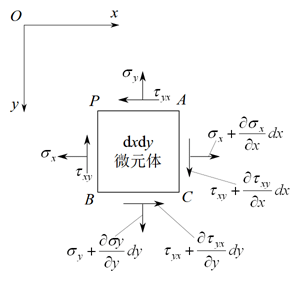
图1 微元体应力示意图
一般而论,应力分量是位置坐标 x 和 y 的函数,因此作用于左右两对面或上下两对面的应力分量不完全相同,而具有微小的差量。为了简化起见,对 AC,BC 的应力用泰勒展开式展开,然后省略二阶无穷小,可得如上图所示的各个应力的大小(或者利用微分可直接计算得到)。
然后列出力矩平衡方程和受力分析。
先是力矩平衡:
\[
{\tau}_{xy} + \frac{1}{2} \frac{\partial {\tau}_{xy}}{\partial x} dx = {\tau}_{yx} + \frac{1}{2} \frac{\partial {\tau}_{yx}}{\partial y} dy
\]
由力矩平衡方程可得剪应力互等定理,即:
\[
{\tau}_{xy} = {\tau}_{yx}
\]
根据受力分析,X 方向受力平衡,则:
\[
(\sigma_x + \frac{\partial \sigma_x}{\partial x} dx)dy \times 1 - \sigma_xdy \times 1 + (\tau_{yx}+\frac{\partial \tau_{yx}}{\partial y}dy)dx \times 1 - \tau_{yx}dx \times 1 + X dx \times dy \times 1 = 0
\]
化简得:
\[
\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + X = 0
\]
Y 方向同理可得:
\[
\frac{\partial \sigma_y}{\partial y} + \frac{\partial \tau_{xy}}{\partial x} + Y = 0
\]
所以至此我们就建立了平面问题的平衡微分方程:
\[
\begin{cases}
\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + X = 0 \\
\frac{\partial \sigma_y}{\partial y} + \frac{\partial \tau_{xy}}{\partial x} + Y = 0
\end{cases}
\]
平衡方程中不含 E、μ,所以方程与材料性质无关,而且整个弹性体内都满足,包括边界。
几何方程
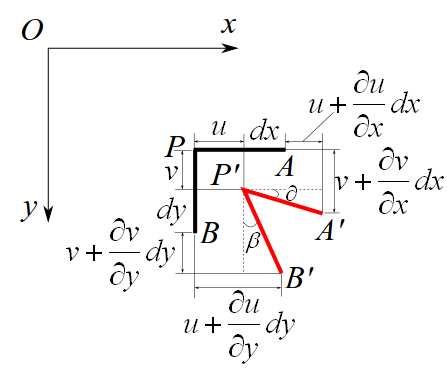
在平面问题中,讨论几何方程也就是讨论应变与位移的关系。
首先考察 P 点邻域内线段的变形:
\[
P \longrightarrow P' \begin{cases} u \\ v \end{cases}
\]
\[
A \longrightarrow A' \begin{cases} u + \frac{\partial u}{\partial x}dx \\ v + \frac{\partial v}{\partial x}dx \end{cases}
\]
\[
B \longrightarrow B' \begin{cases} u + \frac{\partial u}{\partial y}dy \\ v + \frac{\partial v}{\partial y}dy \end{cases}
\]
当然以上几个式子都用了泰勒展开,忽略了二次以上的高阶项。又有 \(PA = dx\),\(PB = dy\)。
在推导公式之前,有必要解释几个概念,正应变,剪应变。何谓正应变,就我的理解,就是相对伸长与原长的比值。剪应变,就是某点两直角线段夹角的变化。
\[
\varepsilon_x = \frac{u + \frac{\partial u}{\partial x} dx - u}{dx} = \frac{\partial u}{\partial x}
\]
\[
\varepsilon_y = \frac{v + \frac{\partial v}{\partial y} dy - v}{dy} = \frac{\partial v}{\partial y}
\]
所以正应变的表达式就是如上所示,至于剪应变,同样可得,只是表达式略微复杂一点。
\[
\gamma_{xy} = \alpha + \beta
\]
\[
\tan \alpha = \frac{v + \frac{\partial v}{\partial x} dx - v}{dx} = \frac{\partial v}{\partial x} \approx \alpha
\]
\[
\tan \beta = \frac{u + \frac{\partial u}{\partial y} dy - u}{dy} = \frac{\partial u}{\partial y} \approx \beta
\]
\[
\gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}
\]
最后整理一下,我们就得到了平面应力问题的几何方程:
\[
\begin{cases}
\varepsilon_x = \frac{\partial u}{\partial x} \\
\varepsilon_y = \frac{\partial v}{\partial y} \\
\gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}
\end{cases}
\]
物理方程
物理方程是根据胡克定律,没错,就是你高中时学过的发现弹簧的弹力 f 和弹簧的长度变化量 x 成正比的那个人。当然我们用到的是广义胡克定律,就是根据胡克定律和泊松比得出来的,推导的话就不写了,随便找本材料力学的书都会有写。
\[
\begin{cases}
\varepsilon_x = \frac{1}{E}[\sigma_x - \mu (\sigma_y + \sigma_z)] \\
\varepsilon_y = \frac{1}{E}[\sigma_y - \mu (\sigma_z + \sigma_x)] \\
\varepsilon_z = \frac{1}{E}[\sigma_z - \mu (\sigma_x + \sigma_y)]
\end{cases}
\]
\[
\begin{cases}
\varepsilon_x = \frac{1}{E}(\sigma_x - \mu \sigma_y) \\
\varepsilon_y = \frac{1}{E}(\sigma_y - \mu \sigma_x)
\end{cases}
\]
以上的是三维的物理方程,二维的话只需要三项:
\[
\begin{cases}
\gamma_{yz} = \frac{1}{G} \tau_{yz} \\
\gamma_{zx} = \frac{1}{G} \tau_{zx} \\
\gamma_{xy} = \frac{1}{G} \tau_{xy} \\
\end{cases}
\]
\[
\gamma_{xy} = \frac{2(1+\mu)}{E} \tau_{xy}
\]
综上所述,弹性力学的基本未知量为三个位移分量,六个应力分量和六个应变分量,共计十五个未知量。基本方程为三个平衡微分方程,六个几何方程和六个物理方程,也是十五个基本方程。因此,可联立这些方程求解未知量。
上一篇: 弹性力学基本假设